Soal dan Pembahasan Matematika IPA SNMPTN 2013 (Kode 138)

Bimbel WIN:

Belajar dari bentuk soal yang sudah pernah ditanyakan membuat persiapan menghadapi ujian yang sebenarnya akan menjadi lebih terarah, lebih fokus dan lebih efektif.

Bentuk soal yang akan diujikan dari tahun ke tahun pada umumnya materinya sama. Pada pelajaran yang menitikberatkan pada hafalan soanya bisa sangat mirip bahkan ada yang persis sama. Sedangkan pada soal hitungan, rumus dan analisanya pada umunya sama.

Oleh karena itu, kami menyarankan bagiadik-adik calon mahasiswa baru (camaba) tahun ini, kuasailah minimal 10 tahun terakhir soal ujian yang sudah pernah keluar.

Pada kesempatan ini, bimbel WIN berbagi soal asli matematika IPA SBMPTN tahun 2013 kode 138 lengkap dengan pembahasannya yang mudah untuk dimengerti. Di akhir pembahasan, kami juga mengajak adik-adik camaba untuk tetap berlatih pada soal online yang sudah kami siapkan, Ayouk teruslah berlatih...!!! Semoga tahun ini kalian semuanya yang belajar disini bisa lolos di pilihan pertama kalian, Amiiin... 🙏🙏

- Matematika IPA -

💦 Soal No.01

Persamaan lingkaran dengan pusat (-1, 1) dan menyinggung garis \(3x - 4y + 12 = 0\) adalah ...

(A) \({x^2} + {y^2} + 2x - 2y + 1{\rm{ }} = {\rm{ }}0\)
(B) \({x^2} + {y^2} + 2x - 2y - 7 = 0\)
(C) \(4{x^2} + 4{y^2} + 8x - 8y - 17 = 0\)
(D) \({x^2} + {y^2} + 2x - 2y - 2 = 0\)
(E) \(4{x^2} + 4{y^2} + 8x - 8y - 1 = 0\)

Pembahasan:

\(g = 3x - 4y + 12 = 0\)

\(\begin{array}{l}r = \left| {\frac{{3( - 1) - 4(1) + 12}}{{\sqrt {{3^2} + {{( - 4)}^2}} }}} \right|\\r = \left| {\frac{{ - 3 - 4 + 12}}{{\sqrt {9 + 16} }}} \right|\end{array}\)

\(\begin{array}{l}{\rm{L}}\, \equiv \,\,\,\,\,\,\,\,\,{\left( {{\rm{x}} - {\rm{a}}} \right)^2} + {\left( {{\rm{y}} - {\rm{b}}} \right)^2}\,\, = {{\rm{r}}^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\left( {{\rm{x}} + 1} \right)^2} + {\left( {{\rm{y}} - 1} \right)^2}\,\,\,\, = {1^2}\\\,\,\,{{\rm{x}}^2} + 2x + 1 + {{\rm{y}}^2} - 2{\rm{y + 1 = 1}}\\\,\,\,{{\rm{x}}^{\rm{2}}} + {{\rm{y}}^2} + 2{\rm{x}} - 2{\rm{y}} + 1\,\,\,\,\,\,\,\,\, = 0\end{array}\)

💥Kunci Jawaban: A

💦 Soal No.02

\(\cot \,\,{105^0} \cdot \tan {15^0}\) = ...

(A) -7 + 4\(\sqrt 3 \)

(B) 7 + 4\(\sqrt 3 \)

(C) 7 - 4\(\sqrt 3 \)

(D) -7 - 4\(\sqrt 3 \)

(E) -7 + 2\(\sqrt 3 \)

Pembahasan:

\(\begin{array}{l}{\rm{co}} + {105^ \circ }\,\,.\,\,{\rm{tan}}\,\,{15^ \circ } = \frac{{\cos \,{{105}^ \circ }}}{{\sin \,{{105}^ \circ }}}\,\,{\rm{x}}\,\,\frac{{\sin \,{{15}^ \circ }}}{{\cos \,{{15}^ \circ }}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{\left( {\sin \left( {{{105}^ \circ } + {{15}^ \circ }} \right) - \sin \left( {{{105}^ \circ } - {{15}^ \circ }} \right)} \right)}}{{\left( {\sin \left( {{{105}^ \circ } + {{15}^ \circ }} \right) + \sin \left( {{{105}^ \circ } - {{15}^ \circ }} \right)} \right)}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{\sin \,\,\,{{120}^ \circ } - \sin \,\,\,{{90}^ \circ }}}{{\sin \,\,\,{{120}^ \circ } + \sin \,\,\,{{90}^ \circ }}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{\left( {\sin \,{{60}^ \circ }} \right) - 1}}{{\left( {\sin \,{{60}^ \circ }} \right) + 1}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{{\textstyle{1 \over 2}}\sqrt 3 - 1}}{{{\textstyle{1 \over 2}}\sqrt 3 + 1}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{\sqrt 3 - 2}}{{\sqrt 3 + 2}}\,\,\,{\rm{x}}\,\,\,\frac{{\sqrt 3 - 2}}{{\sqrt 3 - 2}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{3 - 2\sqrt 3 - 2\sqrt 3 + 4}}{{3 - 4}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{7 - 4\sqrt 3 }}{{ - 1}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = - 7 + 4\sqrt 3 \end{array}\)

💥Kunci Jawaban: A

💦 Soal No.03

Enam anak, 3 laki-laki dan 3 perempuan, duduk sejajar. Peluang 3 perempuan duduk berdampingan adalah ...

(A) \(\frac{1}{{60}}\)

(B) \(\frac{1}{{30}}\)

(C) \(\frac{1}{{15}}\)

(D) \(\frac{1}{{10}}\)

(E) \(\frac{1}{{5}}\)

Pembahasan:

L = laki-laki

P = Perempuan

\(\begin{array}{l}{\rm{n(k)}} = 4\,!\,\,\,\, \cdot \,\,\,\,3\,!\\{\rm{n(s)}} = 6\,!\\\\{\rm{P = }}\frac{{{\rm{n(k)}}}}{{{\rm{n(s)}}}}\\{\rm{P = }}\frac{{{\rm{4}}\,{\rm{!}}\,\,\,\, \cdot \,\,\,\,{\rm{3}}\,{\rm{!}}}}{{{\rm{6}}\,{\rm{!}}}}\\{\rm{P}} = \frac{{3{\rm X}\,\,2{\rm{x}}1}}{{6{\rm{x}}5}}\\{\rm{P}} = {\textstyle{1 \over 5}}\end{array}\)

💥Kunci Jawaban: E

💦 Soal No. 04

Dalam segitiga ABC diketahui

\(\sin A + \cos B = 6\) dan \(3\cos A + 4\sin B = \sqrt {13} \).

Nilai adalah ...

(A) \(\frac{1}{2}\)

(B) \(\frac{1}{2}\sqrt 2 \)

(C) \(\frac{1}{2}\sqrt 3 \)

(D) \(\sqrt 3 \)

(E) 1

Pembahasan:

Diketahui \(\begin{array}{l}\Delta \,{\rm{ABC}}\,\,\,\,\, \to \,\,\,\,{\rm{A}} + {\rm{B}} + {\rm{C}} = 180\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{A}} + {\rm{B}} = 180 - {\rm{C}}\end{array}\)

\(\begin{array}{l}\,{\rm{(i)}}\,\,\,{\rm{3}}\,{\rm{sin}}\,{\rm A} + 4\,\cos {\rm B}\,\,\,\,\,\,\,\, = 6\\\,\,\,\,\,\,\,{\left( {3\,\sin \,{\rm A} + 4\cos {\rm B}} \right)^2} = {6^2}\\{\rm{g}}\,{\rm{si}}{{\rm{n}}^{\rm{2}}}{\rm A} + 24\sin \,{\rm A} \cdot \cos \,{\rm B} + 16{\cos ^2}{\rm B} = 36\\\,{\rm{(ii)}}\,\,\,{\rm{3}}\,{\rm{cos}}\,{\rm A}{\rm{ + 4}}\,{\rm{sin}}\,{\rm B} = \sqrt {13} \\\,\,\,\,\,\,\,{\left( {3\cos {\rm A} + 4\,\sin {\rm B}} \right)^2} = {\left( {\sqrt {13} } \right)^2}\\{\rm{g}}\,{\rm{co}}{{\rm{s}}^{\rm{2}}}{\rm A} + 24\cos {\rm A} \cdot \sin {\rm B} + 16\,{\sin ^2}{\rm B} = 13\end{array}\)

\(\begin{array}{l} \Rightarrow {\rm{g}}\,{\rm{si}}{{\rm{n}}^{\rm{2}}}{\rm A} + 24\sin {\rm{A}}{\rm{.cos}}\,{\rm{B + 16}}\,{\rm{co}}{{\rm{s}}^{\rm{2}}}{\rm{B = 36}}\\\,\,\,\,\,\,{\underline {{\rm{g}}\,{{\cos }^{\rm{2}}}{\rm A} + 24\cos {\rm{A}}\, \cdot \,{\rm{sin}}\,{\rm{B + 16}}\, \cdot \,{{\sin }^{\rm{2}}}{\rm{B = 13}}} _ + }\end{array}\)

\(\begin{array}{l}{\rm{g}}\left( {{\rm{si}}{{\rm{n}}^{\rm{2}}}{\rm{A + co}}{{\rm{s}}^{\rm{2}}}{\rm{B}}} \right){\rm{ + 24}}\left( {{\rm{sinA}}\, \cdot \,{\rm{cosB + cosA}} \cdot {\rm{sinB}}} \right){\rm{ + 16}}\left( {{\rm{si}}{{\rm{n}}^{\rm{2}}}{\rm{B + co}}{{\rm{s}}^{\rm{2}}}{\rm{B}}} \right){\rm{ = 49}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,9 + 24\sin \left( {{\rm{A}} + {\rm{B}}} \right) + 16 = 49\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,24\sin \left( {{\rm{A}} + {\rm{B}}} \right) = 24\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\sin \left( {{\rm{A}} + {\rm{B}}} \right) = 1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\sin \left( {180 - c} \right) = 1\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\sin \,\,{\rm{c}} = 1\end{array}\)

💥Kunci Jawaban: E

💦 Soal No.05

Diketahui A(-3, 0, 0) , B(0, 3, 0) dan C(0, 0, 8). Panjang vektor proyeksi \(\overline {AC} \) ke sektor \(\overline {AB} \) adalah ...

(A) \(2\sqrt 2 \)

(B) \(3\frac{{\sqrt 2 }}{2}\)

(C) \(\frac{{\sqrt 2 }}{3}\)

(D) \(\sqrt 2 \)

(E) \(\frac{{\sqrt 3 }}{2}\)

Pembahasan:

\(\begin{array}{l}\overline {{\rm{AC}}} \,\,\, = \,\,\,{\rm{C}} - {\rm{A}}\,\,\,{\rm{ = }}\,\,\,\left[ {\begin{array}{*{20}{c}}0\\0\\8\end{array}} \right]\,\,\, - \,\,\,\left[ {\begin{array}{*{20}{c}}{ - 3}\\0\\0\end{array}} \right]\,\,\, = \,\,\,\left[ {\begin{array}{*{20}{c}}3\\0\\8\end{array}} \right]\\\overline {{\rm{AB}}} \,\,\, = \,\,\,{\rm{B}} - {\rm{A}}\,\,\,{\rm{ = }}\,\,\,\left[ {\begin{array}{*{20}{c}}0\\3\\0\end{array}} \right]\,\,\, - \,\,\,\left[ {\begin{array}{*{20}{c}}{ - 3}\\0\\0\end{array}} \right]\,\,\, = \,\,\,\left[ {\begin{array}{*{20}{c}}3\\3\\0\end{array}} \right]\end{array}\)

Panjang proy . Vektor \(\overline {{\rm{AC}}} \)

pada \(\overline {{\rm{AB}}} \)

\( = \,\,\,\frac{{\overline {{\rm{AC}}} \,\,\,.\,\,\,\overline {{\rm{AB}}} }}{{\left| {\overline {{\rm{AB}}} } \right|}}\)

\(\begin{array}{l} = \,\,\,\frac{{\left[ {\begin{array}{*{20}{c}}3\\0\\8\end{array}} \right]\,\,\,.\,\,\,\left[ {\begin{array}{*{20}{c}}3\\3\\0\end{array}} \right]}}{{\sqrt {{3^2} + {3^2} + {0^2}} }}\\ = \,\,\,\frac{{\left( {3{\rm{x}}3} \right) + \left( {0{\rm{x}}3} \right) + \left( {8{\rm{x}}0} \right)}}{{\sqrt {18} }}\\ = \,\,\,\frac{9}{{3\sqrt 2 }}\\ = \,\,\,\frac{{3\sqrt 2 }}{2}\end{array}\)

💥Kunci Jawaban: B

💦 Soal No.06

Tranformasi T merupakan tranformasi cerminan terhadap garis y = -2x kemudian dilanjutkan cerminan terhadap garis \(y = \frac{x}{2}\) Matriks penyajian T adalah ...

(A) \(\left( {\begin{array}{*{20}{c}}{ - 1}&0\\0&1\end{array}} \right)\)

(B) \(\left( {\begin{array}{*{20}{c}}1&0\\0&{ - 1}\end{array}} \right)\)

(C) \(\left( {\begin{array}{*{20}{c}}0&1\\{ - 1}&0\end{array}} \right)\)

(D) \(\left( {\begin{array}{*{20}{c}}0&{ - 1}\\{ - 1}&0\end{array}} \right)\)

(E) \(\left( {\begin{array}{*{20}{c}}{ - 1}&0\\0&{ - 1}\end{array}} \right)\)

Pembahasan:

Transformasi T merupakan pencerminan terhadap garis y = -2x dilanjutkan terhadap garis y = \({\textstyle{1 \over 2}}{\rm{x}}\)

Transformasi sembarang titik oleh transformasi T sama dengan pencerminan titik tersebut terhadap titik (0,0), karena garis y = -2x dan y=\({\textstyle{1 \over 2}}{\rm{x}}\) saling tegak lurus dan berpotongan di titik (0,0)

Sehingga :

T = matriks refleksi terhadap titik (0,0)

T = \(\left[ {\begin{array}{*{20}{c}}{ - 1}&0\\0&{ - 1}\end{array}} \right]\)

💥Kunci Jawaban: E

💦 Soal No.07

Diberikan bidang empat beraturan T.ABC dengan panjang rusuk a. Jika titik P adalah titik tengah rusuk AC, maka jarak titik P ke garis BT adalah ...

(A) \(\frac{a}{2}\sqrt 2 \)

(B) \(\frac{a}{3}\sqrt 2 \)

(C) \(\frac{a}{4}\sqrt 2 \)

(D) \(\frac{a}{2}\sqrt 3 \)

(E) \(\frac{a}{3}\sqrt 3 \)

Pembahasan:

\(\begin{array}{l}{\rm{TP = BP = }}\sqrt {{\rm{A}}{{\rm{T}}^2} - {\rm{A}}{{\rm{P}}^2}} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {{{\rm{a}}^2} - {{\left( {{\textstyle{1 \over 2}}{\rm{a}}} \right)}^2}} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {{{\rm{a}}^2} - {\textstyle{1 \over 4}}{{\rm{a}}^{\rm{2}}}} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {\textstyle{1 \over 2}}{\rm{a}}\sqrt 3 \end{array}\)

Jarak titik P ke garis BT

\(\begin{array}{l}{\rm{PO = }}\sqrt {{\rm{P}}{{\rm{T}}^2} - {\rm{O}}{{\rm{T}}^2}} \\\,\,\,\,\,\,\, = \sqrt {{{\left( {{\textstyle{1 \over 2}}{\rm{a}}\sqrt 3 } \right)}^2} - {{\left( {{\textstyle{1 \over 2}}{\rm{a}}} \right)}^2}} \\\,\,\,\,\,\,\, = \sqrt {{\textstyle{3 \over 4}}{{\rm{a}}^2} - {\textstyle{1 \over 4}}{{\rm{a}}^{\rm{2}}}} \\\,\,\,\,\,\,\, = {\textstyle{1 \over 2}}{\rm{a}}\sqrt 2 \end{array}\)

💥Kunci Jawaban: A

💦 Soal No.08

Jika \({x^4} + a{x^3} + (b - 14)x2 + 28x - 15 = f(x)(x - 1)\) dengan \(f(x)\) habis dibagi \((x - 1)\), maka nilai a adalah ...

(A) -4

(B) -2

(C) 0

(D) 2

(E) 4

Pembahasan:

Jika \(f\left( x \right).\left( {x - 1} \right) = {x^4} + a{x^3} + \left( {b - 14} \right){x^2} + 28x - 15\)

(i) artinya (x - 1) adalah faktor linear dari suku banyak \(\left( {{{\rm{x}}^4} + {\rm{a}}{{\rm{x}}^{\rm{3}}} + \left( {{\rm{b}} - 14} \right){{\rm{x}}^2} + 28{\rm{x}} - 15} \right)\)

x = 1 \(\begin{array}{l}1\,\,\,\,a\,\,\,\,\left( {b - 14} \right)\,\,\,\,\,\,\,\,\,28\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 15\\{\underline {\,\,\,\,\,\,1\,\,\,\,\,\,\,\,\,a + 1\,\,\,\,\,\,a + b - 13\,\,\,\,\,a + b + 15} _ + }\\1\,\,\,\,\,\,{\rm{a}} + 1\,\,\,\,\,\,{\rm{a + b - 13}}\,\,\,\,\,{\rm{a + b + 15}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,0\end{array}\)

s (x) = 0 \( \to \)-15 + a + b + 15 = 0

a + b = 0 ... pers (1)

eliminasi pers (1) dan pers (2)

\(\begin{array}{*{20}{c}}{3a + 2b = - 4}\\{a + b = 0}\end{array}\left| {\begin{array}{*{20}{c}}{{\rm{x}}\,1}\\{{\rm{x}}2}\end{array}} \right|\begin{array}{*{20}{c}}{3a + 2b = - 4}\\\begin{array}{l}\underline {2a + 2b = 0\,\, - } \\a = - 4\end{array}\end{array}\)

(ii) f(x) adalah hasil bagi suku banyak

\(\left( {{{\rm{x}}^4} + {\rm{a}}{{\rm{x}}^3} + \left( {{\rm{b}} - 14} \right){{\rm{x}}^2} + 28\,\,{\rm{x}} - 15} \right)\,\,{\rm{oleh}}\,\,\left( {{\rm{x}} - 1} \right)\)

\(\begin{array}{l}{\rm{f}}\left( {\rm{x}} \right).\left( {{\rm{x}} - 1} \right) = \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{f}}\left( {\rm{x}} \right) = \end{array}\) \(\begin{array}{l}{x^4}a{x^3} + \left( {b - 14} \right){x^2} + 28x - 15\\\underline {{{\rm{x}}^4} + {\rm{a}}{{\rm{x}}^3} + \left( {{\rm{b}} - 14} \right){{\rm{x}}^2} + 28{\rm{x}} - 15} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {{\rm{x}} - 1} \right)\end{array}\)

( x - 1 ) merupakan faktor f (x)

x = 1 \(\begin{array}{l}1\,\,\,\,\,{\rm{a}} + 1\,\,\,\,\,{\rm{a + b}} - 13\,\,\,\,\,\,\,\,\,{\rm{a + b}} + 15\\{\underline {\,\,\,\,\,\,\,\,\,\,\,1\,\,\,\,\,\,\,\,\,\,a + 2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,2a + b - 11} _ + }\\1\,\,\,\,\,\,\,a + 2\,\,\,\,\,\,2a + b - 11\,\,\,\,\,\,\,\,\,\,\,\,\,\,0\end{array}\)

s (x) = 0 \( \to \)-15 + a + b + 15 = 0

3a + 2b = -4 pers (2)

💥Kunci Jawaban:

💦 Soal No.09

\(\mathop {\lim }\limits_{x \to 0} \frac{{\cos x - \cos 3x}}{{{x^2}\sqrt {4 - x} }} = ...\)

(A) -2

(B) - 1/2

(C) 1/2

(D) 1

(E) 2

Pembahasan:

\(\mathop {\lim }\limits_{x \to 0} \,\,\,\,\,\frac{{\cos \,\,{\rm{x}} - \cos \,\,3{\rm{x}}}}{{{x^2}\,\,\,.\,\,\,\sqrt {4 - {\rm{x}}} }}\) \(\begin{array}{l} = \mathop {\lim }\limits_{x \to 0} \,\,\,\,\,\,\frac{{ - 2\, \cdot \,\,\sin \left( {{\textstyle{{{\rm{x}} + 3{\rm{x}}} \over 2}}} \right) \cdot \sin \left( {{\textstyle{{{\rm{x}} - 3{\rm{x}}} \over 2}}} \right)}}{{{\rm{x}}\,\,.\,\,{\rm{x}}\,\,.\,\,\sqrt {4 - {\rm{x}}} }}\\ = \mathop {\lim }\limits_{x \to 0} \,\,\,\,\,\,\frac{{ - 2\,.\,{{\sin }^2}\,\,2{\rm{x}}\,\,.\,\,{{\sin }^{ - 1}} - {\rm{x}}}}{{\mathop {\rm{x}}\limits_1 \,\,.\,\,\mathop {\rm{x}}\limits_1 \,\,.\sqrt {4 - {\rm{x}}} }}\\ = \mathop {\lim }\limits_{x \to 0} \,\,\,\,\,\,\frac{4}{{\sqrt {4 - {\rm{x}}} }}\\ = \frac{4}{{\sqrt {4 - 0} }}\\ = 2\,\end{array}\)

💥 Kunci Jawaban: E

💦Soal No.10

Diketahui \(f(x) = \frac{1}{2}{x^3} + {x^2} - 3x + 11\). Jika \(g(x) = f(1 - x)\) maka g naik pada ...

(A) \( - 3 \le x \le 1\)

(B) \(0 \le x \le 2\)

(C) \( - 3 \le x \le 3\)

(D) \(0 \le x \le 5\)

(E) \( - 4 \le x \le 0\)

Pembahasan:

💥 Kunci Jawaban:

💦Soal No.11

\(\int {4\sin x\, \cdot {{\cos }^2}} 2x\,d{\rm{x = }}...\)

(A) \(\frac{1}{5}\cos 5x + \frac{1}{3}\cos 3x - 2\cos x + C\)

(B) \(\cos 5x + \cos 3x - 2\cos x + C\)

(C) \( - \cos 5x + \cos 3x - 2\cos x + C\)

(D) \( - \frac{1}{5}\cos 5x + \frac{1}{3}\cos 3x - 2\cos x + C\)

(E) \( - \frac{1}{5}\cos 5x + \frac{1}{3}\cos 3x + 2\cos x + C\)

Pembahasan:
\(\begin{array}{l}\int {4\,\, \cdot \,\,\sin \,{\rm{x}}\,\, \cdot {{\cos }^2}\,\,2{\rm{x}}\,\,{\rm{dx}} = \int {4\,\, \cdot \,\,\sin \,{\rm{x}}\,\, \cdot \,\,\cos \,2{\rm{x}}\,\, \cdot \cos 2{\rm{x}}\,\,{\rm{dx}}} } \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \int {4\,\, \cdot \,\,{\textstyle{1 \over 2}}\,\, \cdot \left( {\sin \,3{\rm{x}} - \sin \,{\rm{x}}} \right) \cdot \cos \,2{\rm{x}}\,\,{\rm{dx}}} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \int {2 \cdot \sin \,3{\rm{x}} \cdot \cos \,2{\rm{x}}\,{\rm{dx}} - \int {2 \cdot \sin \,{\rm{x}} \cdot \cos \,2{\rm{x}}\,{\rm{dx}}} } \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \int {\left( {\sin \,5{\rm{x}} + \sin \,{\rm{x}}} \right){\rm{dx}} - \int {\left( {\sin \,3{\rm{x}} - \sin \,{\rm{x}}} \right){\rm{dx}}} } \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \left( {{\textstyle{1 \over 5}}\cos \,5{\rm{x}} - \cos \,{\rm{x}}} \right) - \left( { - {\textstyle{1 \over 3}}\cos \,3{\rm{x}} + \cos \,{\rm{x}}} \right) + {\rm{c}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = - {\textstyle{1 \over 5}}\cos \,5{\rm{x}} + {\textstyle{1 \over 3}}\cos \,3{\rm{x}} - 2\,\cos \,{\rm{x}} + {\rm{c}}\end{array}\)
💥 Kunci Jawaban: D

💦 Soal No.12

Luas daerah yang dibatasi oleh kurva \(y = 6 - {x^2}\) dan \(y = 5\,\left| x \right|\) adalah ...

(A) \(\int\limits_0^1 {( - {x^2} + 5x + 6)dx} \)

(B) \(\int\limits_{ - 1}^0 {( - {x^2} + 5x + 6)dx} \)

(C) \(2\int\limits_{ - 1}^0 {( - {x^2} + 5x + 6)dx} \)

(D) \(\int\limits_{ - 1}^1 {( - {x^2} + 5x + 6)dx} \)

(E) \(2\int\limits_{ - 1}^0 {( - {x^2} - 5x + 6)dx} \)

Pembahasan:

Titik Potong

\(\begin{array}{l}{{\rm{y}}_{{\rm{kurva}}}} - {{\rm{y}}_{{\rm{garis}}}} = 0\\\,\,\,\,\,6 - {{\rm{x}}^2} - 5\left| {\rm{x}} \right| = 0\\\,\,\,\,\,{{\rm{x}}^2} + 5\left| {\rm{x}} \right| - 6 = 0\end{array}\)

\(\begin{array}{l}\left( {\rm{i}} \right)\,\,\,\,\,\,{{\rm{x}}^2} + 5{\rm{x}} - 6 = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {{\rm{ii}}} \right)\,\,\,\,\,\,{{\rm{x}}^2} - 5{\rm{x}} - 6 = 0\\\,\,\,\,\,\,\left( {{\rm{x}} + 6} \right)\left( {{\rm{x}} - 1} \right) = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {{\rm{x}} - 6} \right)\left( {{\rm{x}} + 1} \right) = 0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x = - 1\end{array}\)

\(\begin{array}{l}{\rm{L}} = 2 \cdot \int\limits_{ - 1}^0 {\left( {\left( {6 - {{\rm{x}}^2}} \right) - \left( { - 5{\rm{x}}} \right)} \right){\rm{dx}}} \\\,\,\,\, = 2\int\limits_{ - 1}^0 {\left( { - {{\rm{x}}^2} + 5{\rm{x}} + 6} \right){\rm{dx}}} \end{array}\)

💥Kunci Jawaban: C

💦 Soal No.13

Banyak bilangan ratusan dengan angka pertama dan kedua mempunyai selisih 2 atau 3 adalah ...

(A) 300

(B) 280

(C) 260

(D) 252

(E) 150

Pembahasan:

Angka yang tersedia : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 banyak bilangan ratusan

( i ) selisih antara bil. pertama dan bil. kedua = 2

\(\begin{array}{l}2\,\,{\rm{dan}}\,\,0\,|1\,|\,|1\,|\,|10\,|\, = 10\\4\,\,{\rm{dan}}\,\,2\,|1\,|\,|1\,|\,|10\,|\,\, = 10\, \times \,2 = 20\\6\,\,{\rm{dan}}\,\,4\,|1\,|\,|1\,|\,|10\,|\, = 10\, \times \,2 = 20\\8\,\,{\rm{dan}}\,\,6\,|1\,|\,|1\,|\,|10\,|\, = 10\, \times \,2 = 20\\3\,\,{\rm{dan}}\,\,1\,|1\,|\,|1\,|\,|10\,|\, = 10\, \times \,2 = 20\\5\,\,{\rm{dan}}\,\,3\,|1\,|\,|1\,|\,|10\,|\, = 10\, \times \,2 = 20\\7\,\,{\rm{dan}}\,\,5\,|1\,|\,|1\,|\,|10\,|\, = 10\, \times \,2 = 20\\9\,\,{\rm{dan}}\,\,7\,|1\,|\,|1\,|\,|10\,|\, = 10\, \times \,2 = 20\end{array}\)

\(\begin{array}{l}3\,\,{\rm{dan}}\,\,0\,\,|1||1||10|\, = 10\\6\,\,{\rm{dan}}\,\,3\,\,|1||1||10|\, = 10\, \times \,2 = 20\\9\,\,{\rm{dan}}\,\,6\,\,|1||1||10|\, = 10\, \times \,2 = 20\\4\,\,{\rm{dan}}\,\,1\,\,|1||1||10|\, = 10\, \times \,2 = 20\\7\,\,{\rm{dan}}\,\,4\,\,|1||1||10|\, = 10\, \times \,2 = 20\\5\,\,{\rm{dan}}\,\,2\,\,|1||1||10|\, = 10\, \times \,2 = 20\\8\,\,{\rm{dan}}\,\,5\,\,|1||1||10|\, = 10\, \times \,2 = 20\end{array}\)

Total \(\begin{array}{l} = \left( {13 \times 20} \right) + \left( {2 \times 10} \right)\\ = 280\end{array}\)

💥Kunci Jawaban: B

💦 Soal No.14

Diketahui \(f(x) = (a + 1){x^3} - 3b{x^2} - 9x\). Jika \({f^n}(x)\) habis dibagi \(x + 1\), maka kurva \(y = f(x)\) tidak mempunyai titik ekstrem lokal jika ...

(A) -3 < b < 0

(B) -4 < b < -1

(C) 0 < b < 3

(D) -4 < b < 0

(E) 1 < b < 4

Pembahasan:

\(\begin{array}{l}{\rm{F}}\left( {\rm{x}} \right) = \left( {{\rm{a}} + 1} \right){{\rm{x}}^3} - 3\,{\rm{bx}} - 9{\rm{x}}\\{{\rm{F}}^I}\left( {\rm{x}} \right) = \left( {3{\rm{a}} + 3} \right){{\rm{x}}^2} - 6{\rm{b}}\,{\rm{x}} - 9\\{{\rm{F}}^{ll}}\left( {\rm{x}} \right) = \left( {6{\rm{a}} + 6} \right){\rm{x}} - 6{\rm{b}}\end{array}\)

(i) F'' (x) habis dibagi (x + 1)

\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,F\left( { - 1} \right) = 0\\\left( {6a + 6} \right)\left( { - 1} \right) - 6b = 0\\{\underline {\,\,\,\,\,\,\,\,\, - 6a - 6 - 6b = 0} _{: - 6}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,a + 1 + b = 0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,a = - - b\end{array}\)

Kurva F (x) tidak mempunyai titik ekstreem lokal jika turunan pertamanya hanya memiliki paling banyak 1 ekor

\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{F}}'\left( {\rm{x}} \right) = 0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {3{\rm{a}} + 3} \right){{\rm{x}}^2} - 6\,{\rm{b}}\,{\rm{x}} - 9 = 0\\\left( {3\left( { - 1 - {\rm{b}}} \right) + 3} \right){{\rm{x}}^2} - 6{\rm{b}}\,{\rm{x}} - 9 = 0\\{\underline {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 3{\rm{b}}\,{{\rm{x}}^2} - 6\,{\rm{b}}\,{\rm{x}} - 9 = 0} _{:\left( { - 3} \right)}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{b}}\,{{\rm{x}}^2} + 2\,{\rm{b}}\,{\rm{x}} + 3 = 0\end{array}\)

Syarat paling banyak 1 akar syaratnya :

\(\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{D}}\,\, \le \,\,0\\\,\,\,\,\,\,\,\,\,\,\,{{\rm{b}}^2} - 4{\rm{ac}}\,\, \le 0\\4{{\rm{b}}^2} - 4\left( {\rm{b}} \right)\left( 3 \right) \le 0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{\rm{b}}^2} - 3{\rm{b}} \le 0\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{b}}\left( {{\rm{b}} - 3} \right) \le 0\end{array}\)

\({\rm{a}} \le {\rm{b}} \le 3\)

💥Kunci Jawaban:

💦 Soal No.15

Jika L(a) adalah luas daerah yang dibatasi oleh sumbu-X dan parabola \(y = ax + {x^2}\), \(0 \le x \le 4\), maka peluang nilai a sehingga \(\frac{1}{{48}} \le L(a) \le \frac{9}{{16}}\) adalah ...

(A) \(\frac{1}{2}\)

(B) \(\frac{3}{4}\)

(C) \(\frac{5}{6}\)

(D) \(\frac{7}{8}\)

(E) \(\frac{{11}}{{12}}\)

Pembahasan:

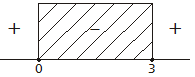
L (a) = luas daerah yang dibatasi oleh sumbu -x dan parabola \(y = {x^2} + ax\) dimana 0<a<2

maka peluang nilai a sehingga \({\textstyle{1 \over {48}}} \le {\rm{L}}\left( {\rm{a}} \right) \le {\textstyle{9 \over {16}}}\)

💥Kunci Jawaban: